How To Rationalize A Numerator

A convention of mathematics is that you don't leave radicals in the denominator of an expression when you write information technology in its terminal class. Thus we do something chosen rationalizing the denominator. This convention makes collecting like terms piece of cake, and your answers will exist truly simplified.

A numerator can contain a radical, but the denominator tin't. The last expression may look more than complicated in its rational form, simply that's what yous have to exercise sometimes.

There are 2 separate situations where radicals may show up in the denominator of a fraction: where expressions comprise 1 radical in the denominator, and where expressions contain two terms in the denominator, at to the lowest degree ane of which is a radical.

Rationalizing with one radical in the denominator

Rationalizing expressions with one radical in the denominator is like shooting fish in a barrel. For example, with a square root, you just need to get rid of the foursquare root. Ordinarily, the best style to practice that in an equation is to square both sides. For example,

Withal, you can't fall for the trap of rationalizing a fraction by squaring the numerator and the denominator. For case, squaring the acme and bottom of

Instead, follow these steps:

Multiply the numerator and the denominator past the same foursquare root.

Any you multiply to the bottom of a fraction, you must multiply to the top; this way, it'due south actually like you multiplied by one and you didn't change the fraction. Hither'south what it looks like:
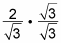
Multiply the tops and multiply the bottoms and simplify.

For this example, you go

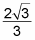
The process for rationalizing a cube root in the denominator is quite similar to that of rationalizing a square root. To go rid of a cube root in the denominator of a fraction, you must cube information technology. If the denominator is a cube root to the kickoff power, for case, yous multiply both the numerator and the denominator by the cube root to the 2nd power to get the cube root to the third power (in the denominator). Raising a cube root to the 3rd power cancels the root — and you're done!

Rationalizing when the denominator is a binomial with at least one radical

You must rationalize the denominator of a fraction when it contains a binomial with a radical. For example, look at the following equations:

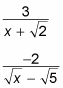
Getting rid of the radical in these denominators involves using the conjugate of the denominators. A conjugate is a binomial formed by taking the opposite of the second term of the original binomial. The conjugate of

The cohabit of x + 2 is x – 2; similarly, the conjugate of

Multiplying a number by its conjugate is really the FOIL method in disguise. Call up from algebra that FOIL stands for first, outside, inside, and last.

The middle 2 terms always abolish each other, and the radicals disappear. For this problem, you get 10 ⁱⁱ – 2.

Take a look at a typical example involving rationalizing a denominator by using the conjugate. First, simplify this expression:

To rationalize this denominator, you multiply the top and bottom by the conjugate of it, which is

The step-past-step breakdown when y'all practise this multiplication is

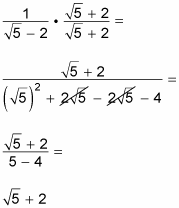
Here's a second instance: Suppose you need to simplify the following problem:

Follow these steps:

Multiply past the conjugate.
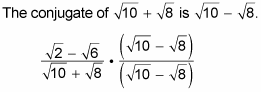
Multiply the numerators and denominators.

FOIL the top and the bottom. (Tricky!) Here'due south how y'all practice it:
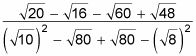
Simplify.

Both the numerator and denominator simplify first to

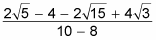
which becomes

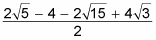
This expression simplifies fifty-fifty further considering the denominator divides into every term in the numerator, which gives you

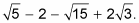
Simplify whatever radical in your last respond — always. For example, to simplify a foursquare root, detect perfect square root factors:

Also, you can add and decrease only radicals that are similar terms. This ways the number within the radical and the index (which is what tells you whether it'south a square root, a cube root, a fourth root, or any) are the same.